ฟังก์ชัน

ฟังก์ชันเป็นบทเรียนที่ต่อจากเรื่องความสัมพันธ์ ในบทเรียนนี้จะได้รู้จักว่าฟังก์ชันเป็นอย่างไร มีเงื่อนไขอย่างไร การแทนฟังก์ชัน ฟังก์ชันจาก A ไป B ฟังก์ชันที่ควรรู้จัก อ่านต่อ

ฟังก์ชันเชิงเส้น

ฟังก์ชันเชิงเส้น (Linear function) 
คือ ฟังก์ชั่นที่อยู่ในรูป f(x) = ax+b เมื่อ a และ b เป็นจำนวนจริง
เช่น f(x) = 2x+1
f(x) = -3x
f(x) = x-5 เป็นต้น อ่านต่อ

ฟังก์ชันกำลังสอง

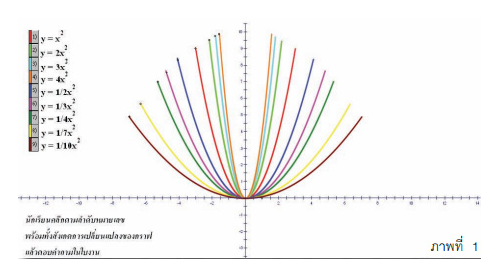
กราฟของฟังก์ชันกำลังสอง   มีชื่อเรียกว่า  พาราโบลา  ซึ่งลักษณะของกราฟของฟังก์ชันขึ้นอยู่กับค่าของ  a , b  และ  c   และเมื่อ  a  เป็นบวกหรือลบ  จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ  และกราฟของฟังก์ชันกำลังสองที่กำหนดด้วยสมการ อ่านต่อ

ฟังก์ชันเอกซ์โพเนนเชียล

ฟังก์ชันนั้นมีอยู่หลายรูปแบบ แต่ละแบบก็มีการตั้งชื่อไม่เหมือนกัน ฟังก์ชันเอกซ์โพเนนเชียลก็เป็นอีกรูปแบบหนึ่งของฟังก์ชันซึ่งเราจะไปดูว่าฟังก์ชันเอกซ์โพนเนนเชียลนั้นมีรูปแบบอย่างไร ก็ต้องไปดูนิยามของมันครับ ว่านิยามของฟังก์ชันเอกซ์โพเนนเชียลนั้นเป็นอย่างไร อ่านต่อ

ฟังก์ชันค่าสัมบูรณ์

ฟังก์ชันค่าสมบูรณ์ถูกกำหนดโดยกฎซึ่งแบ่งออกเป็นสองกรณี

ค่าฟังก์ชันสมบูรณ์ | | จะกำหนดโดย  อ่่านต่อ

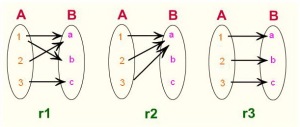
ความสัมพันธ์และฟังก์ชัน

คู่อันดับ (Order Pair) เป็นการจับคู่สิ่งของโดยถือลำดับเป็นสำคัญ เช่น คู่อันดับ a, b จะเขียนแทนด้วย (a, b) เรียก a ว่าเป็นสมาชิกตัวหน้า และเรียก b ว่าเป็นสมาชิกตัวหลัง อ่านต่อ

ฟังก์ชันขั้นบันได

ฟังก์ชันขั้นบันได คือฟังก์ชันบนจำนวนจริงซึ่งเกิดจากการรวมกันระหว่างฟังก์ชันคงตัวจากโดเมนที่แบ่งออกเป็นช่วงหลายช่วง กราฟของฟังก์ชันจะมีลักษณะเป็นส่วนของเส้นตรงหรือรังสีในแนวราบเป็นท่อน ๆ ตามช่วง ในระดับความสูงต่างกัน